Here we have shared some of the Interview Questions asked in PhD Exams, the Experience of Candidates and their Suggestions. Hopefully, this page will be helpful for you in your preparation for PhD Interviews & Exams. This piece of information is shared only for educational purposes.

We request you if you have recently appeared in PhDs Interview or Assistant Prof. Interview or JRF Position Interview, if possible share your Interview Que. /Experience /Suggestions to us for others benefit, Your little contribution can help PhD Aspirants to Prepare themselves.

Send your interview Que/Videos us on maths.whisperer@gmail.com . Subscribe Us On

---

Page Editor: P Kalika & K Munesh

---

PhD Interview Experiences/suggestions: https://www.youtube.com/playlist?list=PLDu0JgProGz4Bnzvq7sRfEsklmGivnkay

---

❤️ We hearty thanks to those persons who shared their Interview Questions & Experiences for others’ help. We wish you all the best for your future.

---

(Added on May 06, 2023)

🎯 PhD Interview questions asked at IIT Ropar (Shared by Bikky Gupta).

“Last I got a mail from IIT Ropar I selected in Phd program, your collection of question give me idea how to prepare for interview, Thank you so much from bottom of my heart. I have question that they ask during my interview. I am attaching here.

---

(Added on May 06, 2023)

🎯 PhD Interview questions asked at IIT Bombay, Kanpur, Jodhpur, Hyderabad, Madras & IISER Pune (Shared by Anik Bhowmick).

‘I am Anik Bhowmick, I have appeared in several PhD interviews this year. I have attached a pdf so that you can share it and help students around the world.’

---

(Added on May 05, 2023)

🎯Interview questions asked at IIT Bombay, Kanpur and NBHM PhD (Anonymously received).

---

(Added on 18-12-2022)

🎯Interview questions at IISER Pune and IIT Guwahati (Anonymously received).

I had given an interview at IIT Guwahati and IISER Pune in the June session. In IISER Pune, they asked questions from linear algebra, ordinary differential equations, real analysis. They are as follows.

1. What is the minimal polynomial. What is the characteristic polynomial.
2. What are the relationship between minimal polynomial and charactestic polynomial. Can you proof those relationships between minimal polynomial and charactestic polynomial.
   In ordinary differential equations, they asked questions from uniqueness and existence theorem. Statement and example of uniqueness theorem.
3. What is the reimann integration. They asked some examples of reimann integration.
4. What is the uniform convergence in sequence of functions.
5. Is continuity implement the uniform convergence of sequence and series of functions. Can you proof it .

During IIT Guwahati, they asked questions from partial differential equations.

1. Write down the general equations of second order pde.
2. What is the heat equations. In heat equations,.what are the parameters.
3. Can you proof the heat equations, from where it is derived .

---

(Added on 30-07-2022)

🎯 NBHM PhD 2022 Interview Questions shared by Bittu Singh.

🎯 CMI PhD Interview experience

(Anonymously Shared)

Student: 1

Student: 2

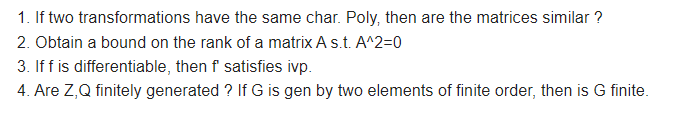
🎯 IISER Pune PhD 2022 July Interview questions shared by Umesh

---

(Added on 04-07-2022)

🎯 PhD Interview/Admission Questions IITB, IITK & IITM

(Anonymously Shared)

IIT Madras Que.

🎯Hello, Sir, Sending PhD interview questions of IISER Bhopal, IIT Indore and IIT Hydrabad.

---

(Added on 28-05-2022)

🎯Hello ! I attended the PhD interview at IIT Dharwad this year. I’m sharing the questions below.

(Anonymous Shared)

1. What is the order of A_n ? Prove your claim.
2. What group is the quotient Gl_n(R)/Sl_n(R) isomorphic to? What about Gl_n(C)/Sl_n(C) ? 
3. What group is the quotient M_n(R)/H isomorphic to ? (H is the set of matrices in M_n(R) with trace 0.)
4. Let H be the group of all 10th roots of unity under multiplication. What group is the quotient (C*,•)/H isomorphic to?
5. G is a finite group such that all its non-identity elements are of order 2. What can you say about G? 
6. Prove that the additive group of a field of order p^n is isomorphic to Zp × Zp × … × Zp (n times).
7. What is the order of Sl_n(Zp) ? Prove it.
8. V is a real vector space. f & g are linear functionals on V such that ker(f) ⊂ ker(g). How are f and g related? 

🎯 PhD test and interview questions collection shared by Nidhi Shukla, Download the PDF file (17Pages).

SNU PhD test

1. The least value of n for which Sn has abelian subgroup of order 30?
2. Co-Variance of two random variable lies between 0 and 1?
3. How to find connected set if set contains element in the form of matrix?
4. A Set containing (x ,y) such that X square + y square is equal to 1 and xy is not equal zero_ compact?
5. T is a mapping from V1to V2 where v1 and V2 are finite dimensional vector spaces let S be a subset of V1 then the relationship between dimension of T(S1) and dimension of S1?
6. The set of all matrices of order n by n, then find the connected matrices in this set??
   1. AA’=A’A=I
   2. trA=1
   3. =>0for all x
7. If a function is given in terms of series then how to find its continuity & Differentiability?

PhD Interview at IITs, IISc, IIPE, etc. Download PDF File: Click here

---

🎯 TIFR Mumbai PhD Interview April 2022 Questions Shared by Dhiman Das.

---

(Added on 07-04-2022)

🎯 Hello Sir,
I am selected for PhD at Aligarh Muslim University. I thank you for all the updates and notes and videos. Sharing my interview questions. Pls keep anonymous. Thank you again for running the kalika community.

(Anonymous Shared)

---

(Added on 30-12-2021)

🎯 PhD Interview 2021 Questions asked at VIT Bhopal

Sir, I have appeared for an Interview for VIT Bhopal on 8th december and also got selected. I am attaching the file of questions here. Also big thanks to you sir as  the collections of interview questions is very helpful for me. and also I am following your study material of many topics for preparing for CSIR & GATE. Regards Suneel Kumar

🎯 PhD Interview 2021 Questions asked at UNIVERSITY OF DELHI

Hey, I have given Interview at UNIVERSITY OF DELHI. The interview questions are follows:
First we have to make a presentation on any of our favourite topic in not more than 8 minutes. My topic was “Fundamental Theorem of Finite Abelian Groups”
The questions asked are as follows:
1) What are elementary divisors? Give an example.
2) Given two finite Abelian Groups G and H. How can we check whether they are isomorphic or not with the help of elementary divisors?
3) What are the future plans that you would like to work with the theorem that you presented?
4) What is the partial converse of Lagrange theorem for Non-Abelian groups that we have from “Fundamental Theorem of Finite Abelian Groups”?
5) How many groups upto isomorphism are there of order 15?
6) What is Cauchy theorem?
7) With the help of Sylow theorem, show that the group of order 15 is Cyclic?
8) Do you know Free Abelian group?
9) What is Commutator group?
10) What are the derived series?
11) With the help of derived series can we define Solvable group?
12) What is Characteristic subgroup?
13) Relation between Characteristic subgroup and Normal subgroup?
14) Why is every characteristic subgroup normal?
15) What is the Commutator subgroup of GL_n(R). Why?

🎯 PhD Interview 2021 Questions asked at IISER MOHALI

Hey, I have given an interview at IISER MOHALI. The questions are as follows:
1) What is the unit group of Z_n? (in terms of n)
2) What are the maximal ideals of Z? (I said of type pZ where p is prime)
3) Prove that Maximal ideals of Z are only of type pZ where p is prime?
4) Consider the complex polynomial ring C[x]. What are its irreducible elements? What are its maximal ideals?
5) Consider C[x,y], what are its maximal ideals?
6) Are the ideals <x-a> and <x-b> in the ring C[x] same? For what condition on ‘a’ and ‘b’ will they be same?
7) Is the space L²[a,b] a Hilbert space?
8) Consider [0,1]. As every point in [0,1] can be written in decimal expansion. Consider the set of all points in [0,1] whose decimal expansion do not include the number 5. What is its measure?

---

(Added on 17-12-2021)

🎯 VIT VELLORE PhD Interview 2021 Questions

Me Nowshad Ali Mir from Jammu and Kashmir. I have appeared for interview on 20th of Oct, 2021 at VIT VELLORE. INTERVIEWERS asked me simple questions:

1. What is Differential Equation? 
2. what is Order of D.E? 
3. Solution of D.E
   1. General Solution 
   2. particular Solution
   3. Singular Solution 
4. Parts of Solution of D.E
   1. Complementary function 
   2. Particular Integral
5. Can C.F alone can be a solution of D.E? 
6. Can P.I alone can be a solution of D.E? 
7. How many arbitrary constants are in General Solution of D.E? 
8. and some questions about my Research Proposal. 

🎯 IIT Kanpur, Madrash, BHU & IISER Berhampur PhD Interview Dec 2021 Questions (Anonymous Share)

(Added on 10-12-2021)

My Name is ———— and I got selected in PhD at IIT Madras for 2022 January session, Here I am attached the following interview questions of mine. Click on the link to read.

🎯 IIT Kanpur PhD Interview December 2021 Questions (Anonymous Share)

1. What can we say about group G if its order is 27?
2. How many non-abelian groups are up to isomorphism of order 27? What about its center?
3. If |G| = p^3(p is prime), show that G has a subgroup of order p^2?
4. Let V be a vector space over C and T: V to V is a linear operator such that for v in V there exists n in N(naturals) satisfying T^n (v) = v. What can be said about the linear operator T? [Hint: Show that T is diagonalizable]

🎯 IIT Bombay PhD Interview Dec 2021 Questions (Anonymous Share)

1. Consider the polynomial f(x) with rational coefficients, then how many homomorphisms are there from Q[x]/<f(x)> to C which maps 1 to 1?
2. Is (Q,+) finitely generated? Explain.
3. Consider the function f(z) = 1/(z^2+1). Is the function entire? Why/Why not. Are there any singularities? Classify them.
4. Consider f(z) = 1/(z^2+1). What is the radius of convergence for the power series about z=100?
5. Give the entire function f such that Re(f(z)) tends to 0 and z tends to infinity.
6. What is a Lipschitz function? Is it continuous?
7. Is the set of all Lipschitz continuous function on [0,1] dense in C[0,1]?
8. Can C[0,1] be approximated by polynomials?

🎯 IIT BHU PhD Interview Dec 2021 Questions (Anonymous Share)

1. Consider the 2×2 matrix that rotates each vector by an angle alpha, then what can be said about its eigenvectors?
2. Can there be a continuous function f:[a,b] to Q(rationals) ?

---

(Added on 01-12-2021)

🎯 IIT Kharagpur PhD Interview 2021 Questions (Anonymous Share)

“Thank you sir for your effort for making us available such questions!” 

The interview was for 30 mins. Area of interest: graph theory.

1st 10 mins, they show the 1st 5 questions which I had to solve in 10mins. Next few questions they asked verbally.

Note: These are the memory based questions. Some small differences may be there.

• What is planar graph?
  • K_4 is planar?
  • K_5?
• What is spanning tree?
• Every graph is tree?
• How can one represent graph in a computer?

🎯 IISc Banglore PhD Interview 2021 Questions (Anonymous Share)

1. Let G be a finite group and G/Z(G) is cyclic then show that G is Abelian.
2. Is the series (n=1 to infinity) [2+sin(n)]/n converge?
3. If f:[0,1] to R is continuous function and Integral from 0 to 1 f(x) dx = 0. Then, does there exists x in [0,1] such that f(x) = 0 ?

---

(Added on 24-11-2021)

🎯 NBHM PhD Interview 2021 Questions (Anonymous Share) (This Student got selected in NBHM).

I am very thankful to Mr. P kalika sir. Your videos helped me a lot.

🎯 Interview Questions for PhD Admission at IIT Hyderabad (Anonymous Share).

Student-1

1) Tell us about your favorite theorem in Linear Algebra. Prove it. Why do you like it?
2) What is the Characteristic Polynomial of a matrix?
3) What is the Rank of the matrix? How do we find it?

Student-2

---

(Added on 19-11-2021)

🎯 Interview Questions for PhD at IIT Jodhpur dated 18-11-2021 (Anonymous Share).

---

---

🎯 NBHM PhD Scholarship 2021 Interview Questions (Anonymous Share) (This Student got selected).

(Added on 07-11-2021)

---

🎯 NBHM Phd Scholarship 2021 Interview & IMSc Phd Admission 2021 Interview Questions (Anonymous Share) (This Student got selected in NBHM).

(Added on 22-10-2021)

I have appeared for BITS Pilani Interview and have been selected in it as well. I don’t remember the questions, but they were just 3-4 and one of them was what is the Nilpotent Group? Interview was very easy.

I have also appeared for the NBHM Phd Scholarship Interview and have been selected.

The questions are as follows:

1. If the order of a group G is >3, then find two automorphisms of G.
2. Can we always find a real polynomial f(x) such that f(1) =2 and f(4) =7? What if f(a) = b and f(c) =d (a,b,c,d are all real)? [Hint: Vandermonde Matrix]
3. Can we always find a real polynomial f(x,y) such that f(1,2) =2 and f(4,7) =9? What if f(a,b) = c and f(d,e) =f (a,b,c,d,e,f are all real)? [Hint: Chinese Remainder Theorem]
4. Given a continuous function f:R to R satisfying f(x+y)=f(x)+f(y). Find f(x). Justify.

I have also appeared for IMSc Phd Interview. The questions are as follows:

1. Given a group G, H is an index 3 subgroup of G. Then either H is a normal subgroup or there exists a subgroup N in H which is normal in G and has index 2 in H.
2. Suppose {a_n} is a sequence of real numbers, fix L in R(real numbers). Assume that for every subsequence {a_n_k} there exists a further subsequence {a_n_k_p} which converges to L. Show that {a_n} is convergent to L.
3. Show that Image of a non-constant entire function is dense in C(complex numbers)?

---

🎯 Some memory based ques from today’s DUET Mphil/PhD exam. (Shared by Kirandeep Kaur)

(Added on 04-10-2021)

Download PDF

---

🎯 Hello sir recently I experienced NBHM PhD interview and sending my interview questions here. (Shared by Parna Saha)

(Added on 22-09-2021)

First they asked my preference and I said abstract algebra.
Then they asked two questions from the nbhm phd written test. One is prove the formula ” number of idempotent elements in Zn = 2^d”
And another one from linear algebra and I answered the question in written exam wrong but still they said to try there…
Then they ask

1. What is class equation?
2. What is the cardinality of center of a group of order 27? Explain it by the help of class equation.
3. Number of Homomorphism from S3 to Z6? Explain.
4. Let A,B are closed sets in R. Consider the set dist(A,B) defined by {|x-y|:x in A,y in B} = 0 then what can you say about the intersection of the sets A and B.
5. One question from topology which I didn’t remember.

Suggestions:
If you are appearing nbhm interview try to read the proofs of the formula we generally use and prepare your nbhm exam questions..all of them
And whatever your preference can be…they ask question from real analysis and topology.

Thank you

🎯 I am attaching here pdf of questions asked in PhD interviews at IIT, IIIT, and IISER. These are collection of questions based on my experience of one year (Shared by Divya).

(Added on 21-09-2021)\

Download PDF shared by Divya: Click Here

---

🎯 Hello here is the question of PhD interview University of Calcutta (Ballygunge Science College) pure Mathematics (Shared by Amitabha Bhattacharya)

(Added on 21-09-2021)

---

---

🎯 IISER Mohali PhD Interview 2021 Questions (Anonymous Share)

(Added on 08-08-2021)

1. Give some examples of non- commutative rings.
2. What are the ideals in the ring M_2(R)?
3. Consider a ring R and an ideal I, and if it contains some invertible element. What is special about this ideal?
4. Let f: C to C is an analytic function. Let P(z) = a_0 + a_1 z + … + a_n z^n is a n degree polynomial. Also P(f) = 0. What can we say about this function?
5. A function function in real is always continuous? If yes then prove. If not then give a counter-example.
6. Which type of discontinuities does an increasing function have?
7. Do we have any homomorphisms from S_3 to Z_6? Justify.
8. Is there a continuous map from [0,1] to (0,1)? Why/Why-not?
9. Construct a surjective map from (0,1) to [0,1].
10. Construct a bijective map from (0,1) to [0,1].

---

🎯 IIIT Delhi PhD Interview 2021 Questions (Anonymous Share)

(Added on 08-08-2021)

1. What is Quotient group? How to define it. What is the equivalence relation here?
2. What is a Factor ring?
3. Let G/H be a factor group. Why do we require H to be a normal subgroup.
4. Give an example of a group G and its non-normal subgroup H such that G/H is not a group.
5. What is a Field Extension?
6. When do we say a field extension is finite?
7. Is every finite field extension algebraic?
8. What about the converse? Give a counter-example. Prove it.
9. What is an Algebraically Closed Field?
10. What is the difference between Algebraic Closure and Algebraically Closed Field?
11. Give an example of an Algebraically Closed Field?
12. Give an example of a non-Algebraically Closed Field?
13. Let p be prime and consider the polynomial 1+x+x^2+…+x^(p-1) over Q. Is it reducible or irreducible. Why
14. What is the splitting field of the above polynomial?
15. What is a general linear group?
16. What is the order of GL(2,Z_p)? How.

---

---

🎯 NIT Patna PhD Interview 2021 Questions (Shared by Soubhik Paramanik)

(Added on 31-07-2021)

---

🎯 NIT Allahabad PhD Interview 2021 Questions (Anonymously Shared)

(Added on 26-07-2021)

1. State existence and uniqueness theorem
2. Define Leibnitz condition
3. y’=siny is linear or non linear? Why?
4. y’=√y what is it’s degree
5. Define regular singular points.
6. Is it possible to find series solution using regular singular point.
7. Define indical equation
8. Value of integration of exp(x²) , limit is from 0 to infinity
9. f(x)=x|x| differentiable at x=0 or not , if yes what is the value of f'(0)
10. How to find tangent plane of f(x,y,z)=0
11. What is equation of plane

---

🎯 IIT INDORE PhD Interview 2021 Questions (Anonymously Shared)

(Added on 23-06-2021)

1. What is dim of R(Q)?
2. Why dimension is infinite?
3. Any n dimension vector space over Q is countable or not
4. f(x) = x sin(1/x) for x≠0, f(x)=0 for x=0Is f(x) continuous ?
5. Why limit of sin(1/x) does not exist at x=0 ?
6. The given function in que 4 is differentiable or not?
7. If the function is continuous then its derivative is continuous?
8. f(x) = x² sin(1/x) for x≠0, = 0 for x=0 is continuous. Then it is differentiable. What if we replace x² by x³?
9. In general f(x) = x^alpha sin(1/x^beta) for  x≠0, = 0  for x=0 Condition on alpha beta for differentiability
10. sin(1/x) as x tends to zero range of limit
11. What is Sturm Separation Theorem?
12. y1=x & y2= sinx then can you form second order differential equation
13. V=P5(x) (R) Let set {1,x}Prove it is LI
14. v1 & v2 are any two vector in 2 dim plane the line joining point v1 & v2 passing through origin is LI or LD

---

🎯 IIT Bhubneswar PhD Interview 2021 Questions (Shared by Radhanandan Mandal).

(Added on 23-06-2021)

---

---

🎯 IIT Jodhpur PhD Interview 2021 Questions (Anonymously Shared)

(Added on 16-06-2021)

1. What is Chinese Remainder Theorem
2. Application of Chinese Remainder Theorem
3. What is Prime Number
4. Chinese remainder theorem in Ring Theory
5. What is an Irreducible Element
6. What you know about set of Integers
7. What is relation in Prime element & Irreducible element

---

🎯 IISc Bangalore PhD Interview 2021 Questions (Thanks to Lalbahadur Sahu)

(Added on 16-06-2021)

---

🎯 IIT Mandi PhD Interview 2021 Questions (Anonymously Shared)

(Added on 15-06-2021)

1. State and explain existence and uniqueness theorem of ODE.
2. What is ODE ? What is PDE ?
3. What is order and degree ?
4. What is characteristics equations ?

---

---

---

🎯 IIT Delhi PhD Stage-1 Interview 2021 Questions (Anonymously Shared)

(Added on 15-06-2021)

🎯 Anonymously Shared – 1

1. Definition of Differentiability
2. f(x) = x sin(1/x) for x≠0, = 0 for x=0 is diff. or not. Prove it.
3. Definition of continuous function. Give an example of Discontinuous function.
4. If A & B are 2×2 matrices such that AB =0 then BA=0 ?
5. In above question, if (AB)²=0 what about BA² ?
6. In group G if every non identity element has order 2 then is it Abelian group? If yes, Prove it.
7. Let G be a group of odd order, F: G to G defined as F(x) = x². Is it a homomorphism? If yes, prove it.

🎯 Anonymously Shared – 2

1. Def. Of open ball.
2. Def. Of closed ball.
3. Def. Of boundary point.
4. [0,1] Union [7,9] center 8 and radius 1 boundary point Or isse related kya puch rahe samajh nhi aaya
5. Complex se fundamental theorem ka proof.
6. Difference between differential function and analytic function.
7. Analytic function, singular point, CR equation, types of singularity, examples of isolated singularity.
8. df/dzbaar = 0 wala result proof kro

🎯 Anonymously Shared – 3

1. If a subring of a ring is integral domain, does it imply Ring is also an integral domain?
2. Definition of Integral domain.
3. A given n×n non invertible matrix will be a zero divisor or not?
4. G=Gl(n, C) , S= set of all n×n invertible diagonal matrices, then
   1. Is S a subgroup of G?
   2. Is S a normal subgroup of G
5. Def of similar matrices
6. does there exist some infinite group having only finite no. Of subgroups?
7. There are infinitely many prime numbers. Proof.
8. If f is non negative continuous function such that [integral (0to1) fdx]=0
9. Then what can u conclude about f?
10. √x is Uc. Why so?

🎯 Anonymously Shared – 4

---

🎯 Interview Questions for PhD Admission 2021 at IISc Bangalore (Shared By Sayan Roy)

(Added on 12-06-2021)

---

---

🎯 Interview Questions for PhD Admission 2021 at IIT Hyderabad (Anonymously Shared)

(Added on 11-06-2021)

I have given an online PhD Interview for IIT Hyderabad. The questions are as follows:

1. Is the collection of all polynomials of degree at most 2 over the field of reals a vector space?
2. Now the function that p(x) goes to its derivative, is it a Linear Transformation?
3. Give its Matrix Representation.
4. Is the matrix diagonalizable? Why/Why not?
5. Prove that a Nilpotent matrix is diagonalizable if and only if it is a zero matrix.
6. Give examples of 2000 (or infinitely) rings.
7. Give infinite examples of fields of characteristic 0.
8. Give infinite examples of Galois extensions.
9. What is the degree of a field extension?
10. What is the degree of the extension Q(w_n) over Q, where w_n is n-th root of unity.

---

🎯 Interview Questions for PhD Admission 2021 at IISER Kolkata (Anonymously Shared)

(Added on 10-06-2021)

---

🎯 PhD Admission 2021 IIT Delhi interview question… (Shared by Sandeep)

(Added on 09-06-2021)

---

🎯 PhD Admission 2021 IISER Kolkata telephonic interview question… (Anonymously Shared)

(Added on 08-06-2021)

1. How many finite algebraically closed fields are there upto isomorphism?
2. how many fields of order 12 are there upto isomorphism?
3. what is caley hamilton theorem?
4. how can we represent all those primes which are of the form -sum of 2 integer.
5. series (n^1/n -1) is convergent or divergent.
   
6. series (n/(n+1))^(1/n) convergent or divergent. ?

---

🎯 PhD Admission 2021 Interview Que. Asked at IIT Mandi (Shared by Dhiman Das)

(Added on 28-05-2021)

● sir maine linear algebra and pde mai interview diya

◆ linear algebra se eigen vector defination

◆ null vector eigen vector ho sakta hai kiya ??

◆ diagonalisibility se and A*A’ diagonalisble or not ase question kiyaa

◆ pde se classifiacation se kuch question kiya

◆ and heat wave de almbert se question kiya sir

---

🎯 PhD Admission 2021 interview Que. Asked at IIT Kharagpur (Anonymously Shared)

1. Expand f(z)=1/z(z-2) by Laurent series expansion in the domain 0<|z|<2 and 2<|z|<infinity.
2. How do these two series differ?
3. What are different iterative methods for solving system of equations?
4. How is Gauss Jacobi method different from Gauss Seidel method?
5. Which of the above has better convergence?
6. When does the Gauss Jacobi method converges?
7. What is meaning of diagonally dominant matrix?
8. Is a diagonally dominant matrix invertibe?
9. Is the function f(x)=x^2-y^2 harmonic?

📚 (Suggestion)👉🏻 Questions asked are easy so one has to be clear about all fundamentals while preparing for interview.

---

🎯 PhD Admission 2021 interview Que. Asked at IISc Banglore (Shared By Sandip)

One of my friends give interview(today) in iisc bangalore for integrated phd..

---

🎯 PhD interview questions Asked at IIT Mandi (Shared by Manisha Agarwal)

(Added on 25-05-2021)

They asked

• Definitions of field, ring, vector space, field extension, linear transformation
• Application of field and field extension
• Collection of all polynomial form a vector space or not?
• Collection of all polynomial of degree greater than or equal to n is subspace or not?
• Collection of all polynomial of deg less than or equal to n form subspace or not?
• If subspace then give any linear transformation on this.

📚 Their Suggestions…

Sir please try to cover latex and mtlab computer applications which we require in phd interview…try to cover as soon as possible.

As they ask that do u know any computer applications like latex and matlab
I think it is also one of the factor so that anyone got selection or not

---

🎯 PhD interview questions Asked at IIT Guwahati (Topic: Real Analysis) (Shared by Harinand Singh)

1. Sequence of function x^n [0, 1] uniform cgt Or not.
2. Above question on [0, 1)
3. Examples of continus function
4. Range of polynomial
5. Example of a nonconstant poly which
6. Rang is bdd.

📚 Their Suggestions …

This was my first interview,
According to me, jisme intersted h us topic ko ache se taiyar kre aur basic bhi.
Maine unhe ode bola but O bole kisi aur me interested h to maine real bola O bs real se hi Sare question puche aur thodi bahut help bhi krte h

---

🎯 PhD Interview Questions Asked at IIT Mandi (Topic: PDE ,& ODE) (Shared by Shadhank)

I have appeared in IIT Mandi PhD interview.

The questions were from topic PDE & ODE.
The questions were as follows:

1. Classify second order PDE with examples of each one? Which type of PDE is classified in these categories (Hyperbolic, Parabolic & Elliptic)?
2. From where the Characteristic Equation comes in such PDE and on the basis of roots of which how we decide the above classification?
3. Classify the homogeneous Laplace Equation in two dimension. (which is also a second order PDE)
4. What is degree and order of a differential equation?
5. What is Initial Value Problem? Why it is called as IVP? Is IVP holds for the differential equation having order greater than one? (Discuss)
6. What is Boundary Value Problem?
7. What are the boundary conditions and how many types of boundary conditions are there? How it it different from Initial Condition?
8. What is Sturm-Liouville’s Problem? Is it regular or not?
9. How many types of BVP? What is regular BVP?
10. Is Heat equation in one dimension an IVP or BVP?

Thats all.

---

🎯 Some of the PhD Interview Questions that were asked to me in the academic year 2020-2021. The interviews were held online (Anonymously Shared)

(Added on 10-05-2021)

Interview Questions in IIT Delhi.(Round 1)

1. Give an example of an ode such that f(x,y) does not satisfy the Lipschitz’ condition, but still a solution exists.
2. What is the most important theorem on finite groups? State and sketch the proof.
3. State Sylow’s Second Theorem.
4. If the Correspondence (aH)(bH)=(abH) defines the binary operation on the Set of distinct left cosets of H in G. Is H a normal subgroup in G?
5. What was the need of an orthonormal basis, when we already had a standard ordered basis?

Interview Questions in IISER Kolkata.(Round 1: Telephonic) 

1. Prove that R is a field if and only if R[x] is a P.I.D.
2. Does R/p become an integral domain if we have only R as a commutative ring without unity and p a prime ideal in R.?
3. Give an explicit form of the prime ideals in the ring Z*Z.
4. If R is a ring such that every subring in R is an ideal in R, prove that R is either isomorphic to Z or isomorphic to Z/nZ.
5. Does there exist a non-commutative ring of order 15? 

Interview Questions in IISER Kolkata.(Round 2: Google Meet)

1. Is every complex matrix diagonalizable?
2. Prove that rank(A*A)=rank(A).
3. Relation between the minimal and characteristic polynomial of similar matrices.
4. If G and H are Abelian groups, M and N are their subgroups respectively, such that G is isomorphic to H, M is isomorphic to N, then is G/M isomorphic to G/N?
5. Let f be an onto ring homomorphism from a PID R to an Integral domain S, such that f is not injective, prove that S is a field.
6. what is the dimension of R[x,y]/<x^3,y^2> as a vector space over R?
7. How many irreducible polynomials are there in Z_2[x]?
8. Show that in a finite group of odd order every element has a unique square root.
9. Prove that the image of a non constant entire function is dense in C.

---

🎯 This Interview Experience is Shared by Gautam Kaushik (PhD Aspirant 2021 ).

---

🔢 PhD Interview Questions Shared by ‘Ritika Das’ (PhD Aspirant 2021 ).

Interview Questions Asked at Visva Bharati University, Kolkata.

---

🎯 PhD Interview Questions & Suggestions Shared by ‘Prince Bharti’ (PhD Aspirant 2021 ).

I admitted PhD in January 2021 session at Hyderabad Central University.

I selected subjects for interview namely Differential equations and Fuzzy Theory. Because I do project in MPhil on Fuzzy Theory so it’s beneficial for me. They ask some questions about my project.

And from Differential equations they ask from SLP and BVP , what is the difference between them, and example of these, and knowledge about boundary conditions that’s it.

Thank you sir 🙏

📚 (Our Question) Any Suggestions from your Side…

Yes sir according to me , interview k liye apna ek subject tyyar kr ke jana chahiye, or uske main main topics per command ho and given conditions , related examples ko dhyan se smajhna kafi halpful rhega. Jiska nhi pta use dheere se sorry bol de or apni pasand ka topic unhe bta do bss , ab aap tyyar rhe sb kuch usi me se poocha jane wala h😊😊 that’s it. Thank you sir.

Ye bhi add kr lena, aapke notes kafi useful rhe mere addmission m , thank you very much sir 🙏 , isi tarah se hmari help krte rhiye …

---

🎯 PhD Interview Questions & Suggestions Shared by ‘Sanket’ (PhD Aspirant 2021 ).

Recently I’ve appeared for VIT Vellore and BITS Pilani interview. Here I’m providing my Interview Questions in handwritten format…

📚 (Our Question) Any Suggestions from your Side…

” Just prepare some basics … Means whatever you are going to tell about research interests. Prepare basics nicely. Prepare one favourite theorem. Lots of example and counter examples”

---

🎯 PhD Interview Questions & Suggestions Shared by ‘Sanjeev‘ (PhD Aspirant 2021 ).

---

Hello sir
I was asked few questions in Tezpur Univ phd interview

1. Shift operators
2. Formula for Sequence of rationals that converges to a given irrational c
3. Difference between hamel and schauder bases and benefits or need of schauder basis
4. Idea of Cantor’s set and its prop and proof sketch of some of the prop
5. Basic on group theory

Thank you very much for providing useful tips and updating us on events happening in Mathematical world.

📚 (Our Question) Any Suggestions from your Side…

Hello Sir…my suggestions are
One may clear the competitive exams but clearing interview is completely different. We need to have good knowledge of topics. Must read standard books (including proofs) like Bartle for Analysis, Gallian for Algebra, etc. Avoid random guess because one wrong answer would expose all your weaknesses. If you don’t know the answer them simply say I can try try and after try if could not get answer then say that you don’t know the answer… Logical implications must be sound.

Note: This page is under construction…

Related Links: